Below the 100 plus Civil Engineering MCQs, which were asked in various exams of civil Engineering like Upsc ESE, Gate and state AEs and JEs with Difficulty Level 2. you can use these multi choice questions to check your preparation and to do Practice.
Question 1. (Force Analysis)
The load shared by the member BC of the structure shown in figure below is
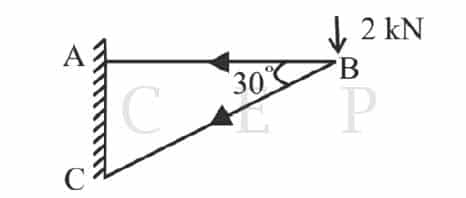
Previously Asked in : TNPSC AE 2012 ||
2√3 KN
3√2 KN
4 KN
3 KN
Answer (Detailed Solution Below)
Option 4 KN is correct
Detailed Explanation :
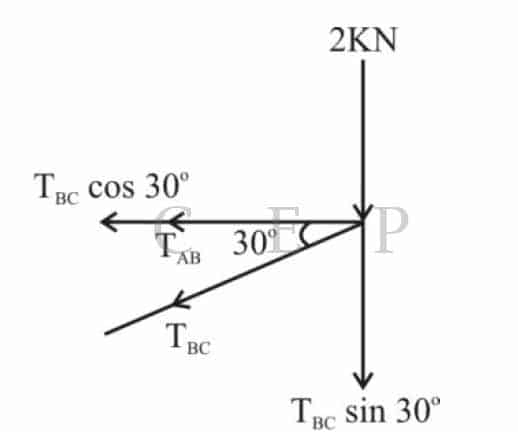
As shown above figure the value of TBC force is
TBC sin30° = – 2 KN
TBC = -2 / sin30° = 4 KN (Compressive)
Question 2. (Force Analysis)
A force p of 50 N and another force Q of unknown magnitude act at 90° to each other. They are balanced by a force of 130 N. The magnitude of Q is
Previously Asked in : ||
60 N
80 N
100 N
120 N
Answer (Detailed Solution Below)
Option 120 N is correct
Detailed Explanation :
Given that : P = 50N ; θ = 90° ; Resultant force (R) = 130N.
we known that ;
Resultant force (R) = √ (P2 +Q2 + 2PQcosθ)
Put the given value in above equation;
130 = √ 502 +Q2 + 2 x 50 x Q x cos90°)
On Squaring both side; Also we know that cos90° = 0
⇒ 1302 = 502 + Q2
⇒ 16900 = 2500 + Q2
⇒ Q2 = 16900 – 2500
⇒ Q2 = 14400
⇒ Q = √ (14400)
Q = 120 N
Hence 120 N option is correct
Question 3. (Force Analysis)
If the resultant of two forces has the same magnitude as either of the force, then the angle between the two forces is
Previously Asked in : ESE PRE 1998 || UP TGT Mathematics 2016 || UPPSC Polytechnic Lecturer Civil 22 Dec 2021
30°
45°
60°
120°
Answer (Detailed Solution Below)
Option 120° is correct
Detailed Explanation :
Concept:
When two forces ‘P’ and ‘Q’ have the same magnitude as their resultant ‘R’, the relationship can be expressed by Parallelogram law of vector addition,. The magnitude of the resultant force is given by:
Resultant force (R) = √ (P2 +Q2 + 2PQcosθ)
Calculation:
Let us consider two forces P” and ‘Q’.
Given that; R = P = Q
Let the angle between P and Q is θ
Using parallelogram law;
R = √ (P2 +Q2 + 2PQcosθ)
R = √ (R2 +R2 + 2R.R.cosθ)
R = √ (2R2 (1+ cosθ)
Squaring both sides gives;
R2 = 2R2 (1+ cosθ)
1/2 = 1 + cosθ [by crossing and shifting]
cosθ = -1/2
θ = cos-1(-1/2)
therefore; θ=120°
Question 4.
coming soon
Question 5.
coming soon
Question 6.
coming soon
Question 7.
coming soon
Question 8.
coming soon
Question 9.
coming soon
Question 10.
coming soon
Please Help us to make it error free. So if you found any kind of error/mistake, do report us by click here or drop a Mail @ admin@civilenggpro.com